雪崩光电二极管冲击电离事件空间分布理论
2021年12月15日
雪崩光电二极管冲击电离事件空间分布理论
2021年12月15日
David A. Ramirez, Majeed M. Hayat,新墨西哥大学电子与计算机工程系和高技术材料中心;
是安德鲁·s·亨廷顿和乔治·威廉姆斯,Allegro微系统公司雷竞技竞猜下载
本文基于:D. A. Ramirez, M. M. Hayat, A. S. Huntington和G. Williams,“雪崩光电二极管冲击电离事件的空间分布理论”,2012年IEEE光子学会议,2012,pp. 100-101, doi: 10.1109/IPCon.2012.6358508。©2012 ieee。本材料允许个人使用。在任何当前或未来的媒体中,所有其他用途都必须获得IEEE的许可,包括为了广告或促销目的而复制/重新发布本材料,创建新的集体作品,转售或重新分发到服务器或列表,或在其他作品中重用本作品的任何版权组件。
雪崩光电二极管(apd)广泛应用于直接检测、高数据速率光纤通信系统以及现代激光雷达系统中。人们已经探索了各种方法来降低APD的过量噪声,这是对APD提供的随机雪崩增益的不确定性的度量。这些方法包括使用薄增殖区域[1]和冲击电离工程(I2E)乘法区域。这两种结构都利用死区效应来减少多余的噪声。另一种方法是抑制空穴的冲击电离,β→0,(或电子,α→0),使空穴与电子的电离比k = β/α尽可能地不同,这也将有助于降低多余的噪声因子。因此,人们对通过冲击电离工程抑制单一载流子冲击电离的APD结构越来越感兴趣。在这些结构中,一种载流子的冲击电离抑制是通过合理地设计异质结倍增区的不同层和其中的电场剖面来实现的。要理解这种多层倍增区域的运作和优化它们的设计,一个关键挑战是分析确定电子和空穴触发冲击电离事件的位置的能力。
本文报道了死空间倍增理论(DSMT)的一个扩展,它能够确定任意异质结倍增区域的冲击电离的空间分布。新开发的递归方程允许确定在乘法区域的任意子区域中由电子和空穴触发的冲击电离事件的数量。此外,该模型可以包含一个松弛机制,以抑制由一种载流子引发的冲击电离。通过数值求解扩展的载流子电离递归方程,计算了两种不同情况下碰撞电离的空间分布:空穴注入InP同构结倍增区;电子注入的InAlAs/InAlGaAs I2E倍增区。后一种结构通过声子散射引入空穴弛豫机制来抑制空穴引发的电离。
在恒定电场作用下,产生平均雪崩增益约900的InP倍增区为1µm,由电子和空穴发起的冲击电离在倍增区的分布如图1所示。假定在x = 0处注入孔。从图中可以看出,空穴和电子触发的电离事件数向倍增区相反的两端增加。当空穴接近x = 1000 nm时,空穴引发的冲击电离数增加;当电子接近x = 0时,电子引发的冲击电离数增加。这一发现与空穴和电子从相反方向的电场中获得动能的事实是一致的,并且可以启动电离的某一特定类型的载流子的数量在运动方向上积累。
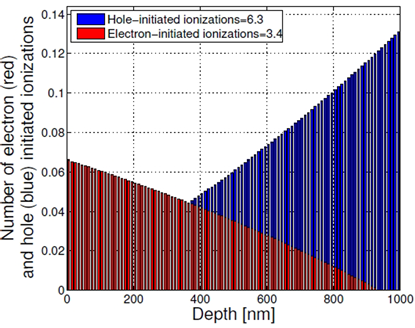
图1:由电子(红色)和空穴(蓝色)引发的冲击电离的空间分布。
我们还计算了具有多级InAlAs/ InAlGaAs I的APD碰撞电离事件的空间分布2E的乘法区域。穿过乘法区域的电场剖面如图2所示,该区域有五个乘法单元,每个单元由一个雪崩层、一个空穴弛豫层和一个电子加热层组成。前两个倍增单元和单元内相应层的电场剖面如图2所示。在这个乘法区,电子在x = 0处被注入。
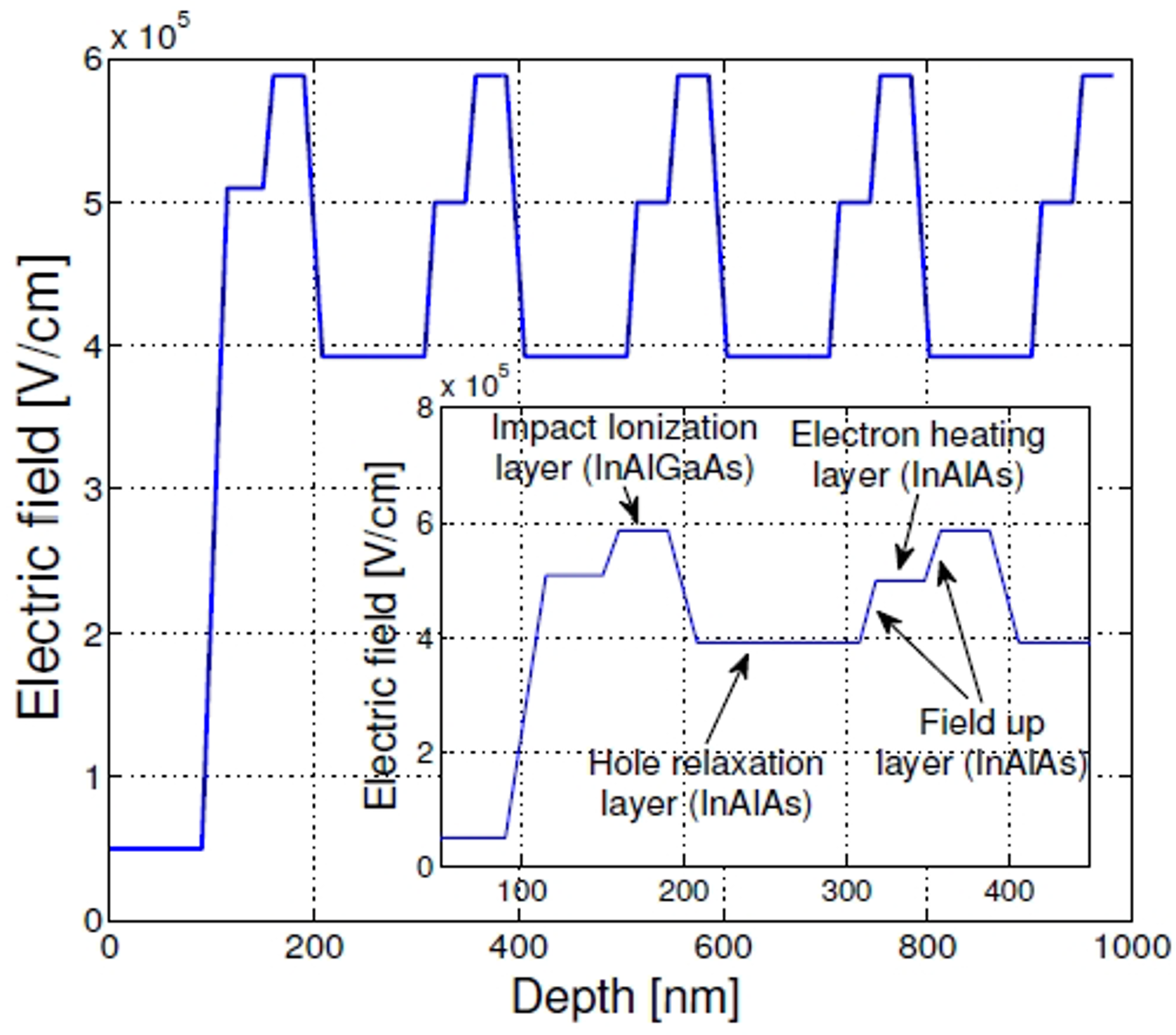
图2:I2E的乘法区域。
由电子和空穴引起的冲击电离在I的倍增区分布2E的乘法区域如图3所示。从图中可以看出,大多数冲击电离事件发生在低带隙和高电离率层(InAlGaAs),这是电场最大的层。
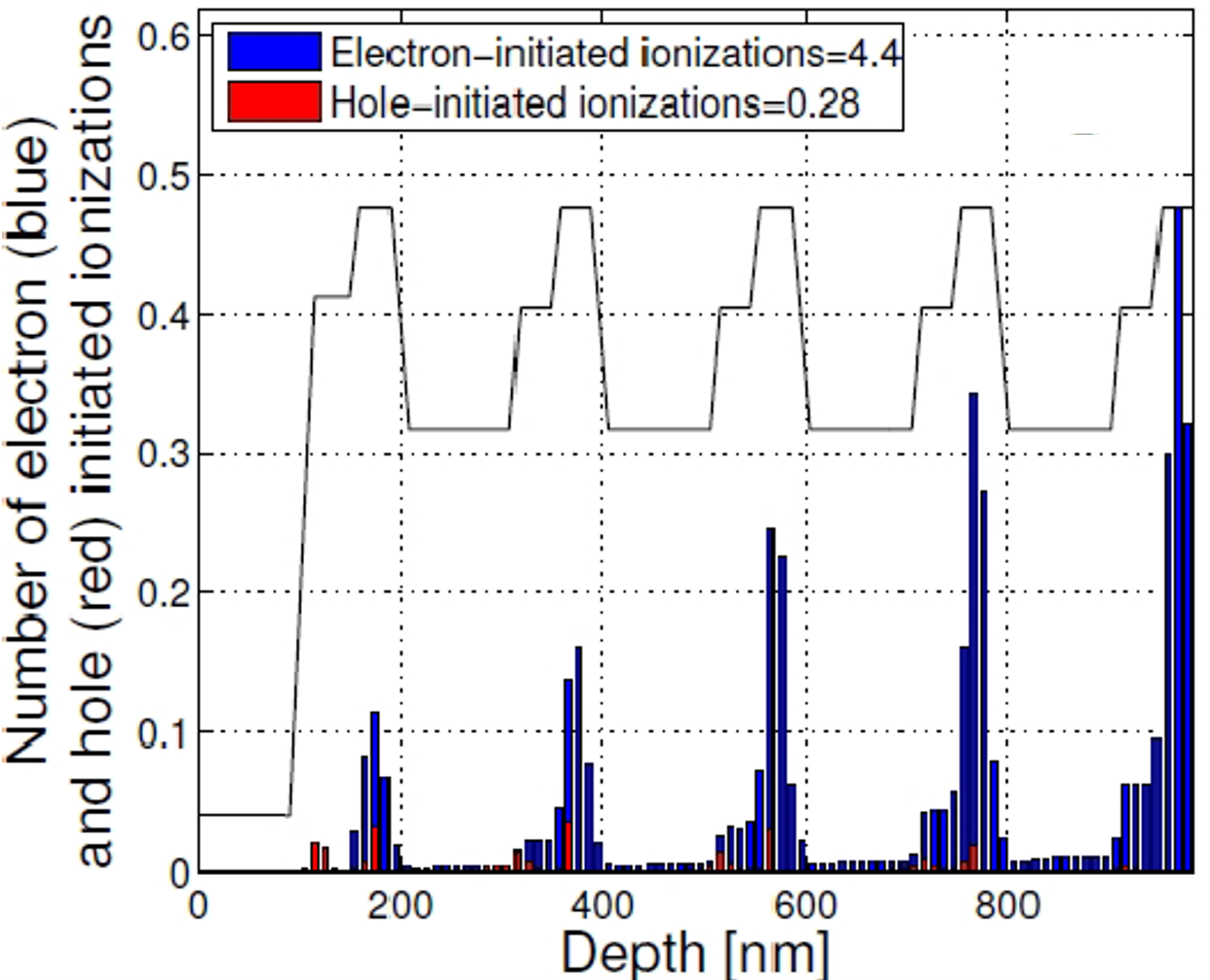
图3:由电子(蓝色)和空穴(红色)引发的冲击电离的空间分布。
撞击电离的空间分布的放大视图如图4所示。该图显示了电子引发的电离数与空穴引发的电离数之间的巨大差异。这是空穴弛豫层的结果,它阻止空穴获得足够的动能来冲击电离,从而减少多余的噪声。
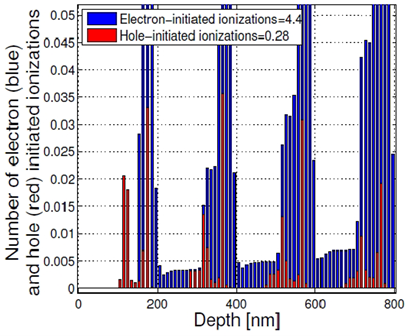
图4:图3的放大视图。
总之,我们建立了一个解析递归模型来计算由空穴和电子在乘法区域内任意位置触发的冲击电离事件的分布。该模型可用于模拟一种载体触发的冲击电离抑制机制,并确定其对冲击电离事件分布的影响。
[1]哈亚特等人。IEEE反式。电子发展,770 - 781(2002)。
[2]S. Wang等。量子电子。, 375 - 378(2003)。
[3]M. Hayat等。电子发展,2114 - 2123(2002)。
[4]W. Sun等。量子电子。, 528 - 532(2012)。
[5]J. Gordon等人。电子学报,519 - 519(1979)。
